| 対象 | 説明 |
| 信号 | 縦軸を振幅、横軸を時間とした波形情報を周波数の分布に変換する |
| 画像 | 縦軸を1ピクセルあたりの画素強度、横軸を座標として、ピクセル間の強度値変化を周波数分布に変換する |
画像に対するフーリエ変換のピクセルあたりの画素強度の例として、1×7サイズのグレースケール画像を考える。例えば下記のようなもの(ここでは視認性のため、拡大した画像で表示)。
画素強度値は明るいほど値が大きい。つまりグレースケールの255階調で考えれば、白い箇所は255、黒い箇所は0の値となる。先ほどの画像にピクセル毎に強度値を重ねて表示すると下記のような値を持つ。
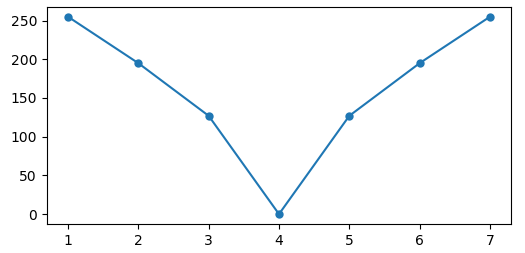
上記画像の強度値を、縦軸を1ピクセルあたりの画素強度、横軸を座標として表しなおしたグラフが下記。画像に対するフーリエ変換はこのグラフに対して行っていることになる
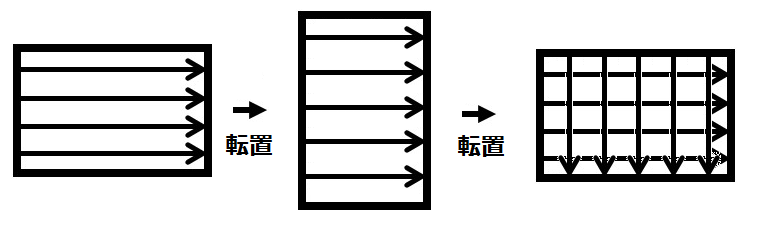
ただし通常画像はもっと大きなサイズであり、1ピクセル高ということはない。そのため、実際には各ピクセル行に対してフーリエ変換を行う。各行へのフーリエ変換の実施後はデータを転置し、転置後のデータに対して再度各行に対してフーリエ変換を実施する。その後再度転置を行いデータの向きを元に戻す作業を行う。これで画像に対する2次元フーリエ変換となる。
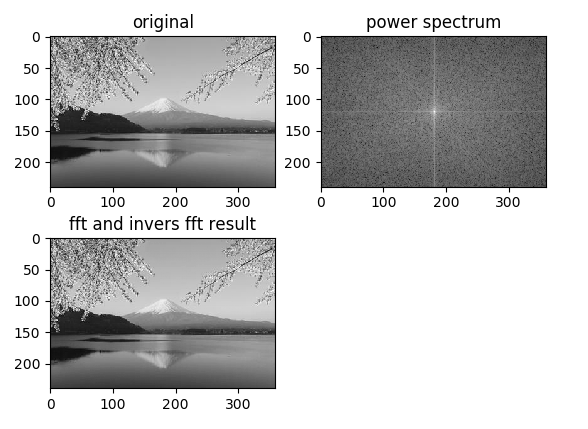
ここまでの内容をpythonコードにしたものが下記。
import cv2
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
image = cv2.imread("mt_fuji.jpg", 0)
h, w = image.shape
ff = np.zeros(image.shape, dtype=complex)
for i in range(h):
ff[i] = np.fft.fft(image[i])
ff = ff.T
for i in range(w):
ff[i] = np.fft.fft(ff[i])
ff = ff.T
fimg = np.fft.fftshift(ff)
mag = 20*np.log(np.abs(fimg))
dst = np.fft.ifft2(ff)
dst = dst.real
dst = np.uint8(dst)
plt.subplot(221)
plt.title("original")
plt.imshow(image, cmap = 'gray')
plt.subplot(222)
plt.title("power spectrum")
plt.imshow(mag, cmap = 'gray')
plt.subplot(223)
plt.title("fft and invers fft result")
plt.imshow(dst, cmap = 'gray')
plt.show()
