Uncategorized – Python in the box

1月 13, 20221月 14, 2022

乱数を使って円周率もどきを求める

乱数を使った円周率もどきを求めてみる

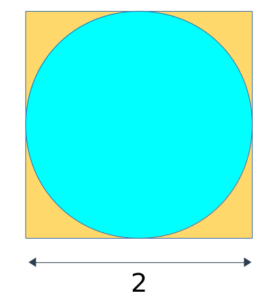
下記のような正方形と内接する円を考える。正方形の1辺は２としておく。この正方形の中にランダムに点を打った際、円の中にも入る確率は円の面積 / 正方形の面積。つまり、確率 = π / 4 となる。

π = 正方形内にランダムに点を打った際に円の中に入る確率は × 4

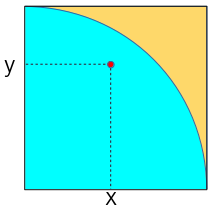
ランダムに打った点が円の中に入ったかどうか？はｘ座標とｙ座標にそれぞれ0～1の乱数を与えてやり、sqrt(x^2 + y^2) が1以下であれば円の中といえる。

この処理を実装したものが下記

import random
import math
import time

def calc_rad (x, y):
  return math.sqrt(x*x +  y*y)


def calc_pi ( NN ):
  num  = 0
  in_n = 0
  while num < NN:
    x = random.random()
    y = random.random()
    if calc_rad (x, y) <= 1:
      in_n = in_n  + 1
    num = num + 1

  return ( in_n / num ) * 4


if __name__ == "__main__":
  for j in range (1,9):
    NN = 10 ** j
    start_time = time.perf_counter()
    pi = calc_pi(NN)
    execution_time = time.perf_counter() - start_time
    delt = math.fabs(math.pi - pi)
    print (str(NN).rjust(10),"  ",f'{pi:11.010f}',"  ",f'{delt:7.06f}',"  ",execution_time)

import random

import math

import time

def calc_rad (x, y):

return math.sqrt(x*x + y*y)

def calc_pi ( NN ):

num = 0

in_n = 0

while num < NN:

x = random.random()

y = random.random()

if calc_rad (x, y) <= 1:

in_n = in_n + 1

num = num + 1

return ( in_n / num ) * 4

if __name__ == "__main__":

for j in range (1,9):

NN = 10 ** j

start_time = time.perf_counter()

pi = calc_pi(NN)

execution_time = time.perf_counter() - start_time

delt = math.fabs(math.pi - pi)

print (str(NN).rjust(10)," ",f'{pi:11.010f}'," ",f'{delt:7.06f}'," ",execution_time)

実行結果

試行回数結果　　　　　　誤差　　　　　処理時間[sec]

10 3.6000000000 0.458407 1.1099999937869143e-05

100 2.9600000000 0.181593 4.040199928567745e-05

1000 3.0800000000 0.061593 0.0004007130000900361

10000 3.1616000000 0.020007 0.004138636999414302

100000 3.1487600000 0.007167 0.042758481000419124

1000000 3.1437800000 0.002187 0.4172533930004647

10000000 3.1411992000 0.000393 4.038885087000381

100000000 3.1415664400 0.000026 41.15365210999971

それなりに近い値かな？

1月 10, 20221月 10, 2022

centos7にてpycudaをインストール(pip3)

pycudaを下記コマンドからインストールを試したところ、、、

1 2	pip3 install pycuda

エラーでストップ。
pycudaのコンパイル時にcuda.hがないとのメッセージで死んでいる。

このエラーについてググるとコンパイル時のPATH/
CPATH/LIBRARY_PATH等にcudaのpathを追加で
対応可能と出てくるが自分の環境では改善せず。。

自分のところでは、gccのバージョンを上げることでエラーが消えて
インストール成功した。gccの対応バージョンがあるっぽい。

エラー時：gcc version 4.8.5 20150623
成功時　：gcc version 7.3.1 20180303

1月 9, 20221月 9, 2022

centos7にcudaをインストール

CUDAはNVIDIAが開発・提供しているGPU向けの汎用並列コンピューティングプラットフォーム。専用のC/C++コンパイラ (nvcc) やライブラリ (API) などが提供されている(wiki)。

NVIDIAのサイトからOS/アーキテクチャにあったToolkitをダウンロード。
https://developer.nvidia.com/cuda-downloads

※wget方式でのコマンドラインが指定される。

1 2	wget https://developer.download.nvidia.com/compute/cuda/11.5.1/local_installers/cuda_11.5.1_495.29.05_linux.run sudo sh cuda_11.5.1_495.29.05_linux.run

acceptと入力してEnter

とりあえず全部にチェック入れてInstall

インストールの際はUIをGUIからCUIに変更しておく(参考)。

インストールした結果が下記

2月 17, 2017

UbuntuのPythonでpyQtGraphをインストール

作業メモ
まずはUbuntuにてeasy_installをpipをインストール

easy_installのインストール
$ sudo apt-get install python-setuptools

pipのインストール
$ sudo apt-get install python-pip

pipを使ってpyQtGraphをインストール
$ sudo pip install pyqtgraph

2月 11, 20171月 7, 2022

分子動力学による粒子のシミュレーション

粒子の動きを分子動力学で計算しmatplotlibで可視化してみる。
ただし各粒子間には相互作用は働かないシンプルな系として考える。
速度の計算はベルレ法(参考)。

各粒子はお互いが見えていないので、初速のまま真っ直ぐに飛び続ける。境界を越えたら反対側へ。

#-*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import random

a  = 10
Dt = 0.1

#Define xy index
PX = 0
PY = 1
VX = 2
VY = 3
FX = 4
FY = 5

def integ(xy):
  #verlet integration
  particle_num = len(xy)
  pnum = 0
  while pnum < particle_num:
    #update velocity
    xy[pnum][VX] = xy[pnum][VX] + 0.5*Dt*xy[pnum][FX]
    xy[pnum][VY] = xy[pnum][VY] + 0.5*Dt*xy[pnum][FY]
    #update position
    xy[pnum][PX] = xy[pnum][PX] + Dt*xy[pnum][VX]
    xy[pnum][PY] = xy[pnum][PY] + Dt*xy[pnum][VY]
    #boundary condition
    if xy[pnum][PX] > a:
       xy[pnum][PX] -= a
    if xy[pnum][PY] > a:
       xy[pnum][PY] -= a
    if xy[pnum][PX] < 0:
       xy[pnum][PX] += a
    if xy[pnum][PY] < 0:
       xy[pnum][PY] += a
    pnum += 1


def update(i, fig_title, xy, total_step):
    if i != 0:
        plt.cla()
    ax.set_xlim(0,10)
    ax.set_ylim(0,10)
    integ(xy)
    nnum = 0
    while nnum < len(xy):
       plt.plot(xy[nnum][PX], xy[nnum][PY], "o")
       nnum = nnum + 1
    plt.title(fig_title + ' step = ' + str(i) + '/' + str(total_step))


def init_set(xy):
  pnum = 0
  xv_sum = 0
  yv_sum = 0
  particle_num = len(xy)
  while pnum < particle_num:
    xy[pnum][PX] = 0  # x-position
    xy[pnum][PY] = 0  # y-position
    xy[pnum][VX] = random.uniform(-1,1) # x-velocity
    xy[pnum][VY] = random.uniform(-1,1) # y-velocity
    xv_sum += xy[pnum][VX]
    yv_sum += xy[pnum][VY]
    xy[pnum][FX] = 0   # x-force
    xy[pnum][FY] = 0   # y-force
    pnum += 1
  #Total momentum to zero
  xv_sum = xv_sum / particle_num
  yv_sum = yv_sum / particle_num
  pnum = 0
  while pnum < particle_num:
    xy[pnum][VX] = xy[pnum][VX] - xv_sum
    xy[pnum][VY] = xy[pnum][VY] - yv_sum
    pnum += 1


if __name__ == "__main__":
    fig = plt.figure(figsize = (10, 6))
    fig.set_size_inches(10,10)
    ax = fig.add_subplot(111)
    perticle_num = 100
    xy = [[0 for i in range(6)] for j in range(perticle_num)]
    init_set(xy)
    total_step =400
    ani = anm.FuncAnimation(fig, \
                        update, fargs = ('Molecular Dynamics ', xy, total_step), \
                        interval = 10, frames =  total_step)
    plt.show()
    #ani.save("Sample_MD.gif", writer = 'imagemagick', dpi=50)

#-*- coding:utf-8 -*-

import matplotlib.pyplot as plt

import numpy as np

import random

a = 10

Dt = 0.1

#Define xy index

PX = 0

PY = 1

VX = 2

VY = 3

FX = 4

FY = 5

def integ(xy):

#verlet integration

particle_num = len(xy)

pnum = 0

while pnum < particle_num:

#update velocity

xy[pnum][VX] = xy[pnum][VX] + 0.5*Dt*xy[pnum][FX]

xy[pnum][VY] = xy[pnum][VY] + 0.5*Dt*xy[pnum][FY]

#update position

xy[pnum][PX] = xy[pnum][PX] + Dt*xy[pnum][VX]

xy[pnum][PY] = xy[pnum][PY] + Dt*xy[pnum][VY]

#boundary condition

if xy[pnum][PX] > a:

xy[pnum][PX] -= a

if xy[pnum][PY] > a:

xy[pnum][PY] -= a

if xy[pnum][PX] < 0:

xy[pnum][PX] += a

if xy[pnum][PY] < 0:

xy[pnum][PY] += a

pnum += 1

def update(i, fig_title, xy, total_step):

if i != 0:

plt.cla()

ax.set_xlim(0,10)

ax.set_ylim(0,10)

integ(xy)

nnum = 0

while nnum < len(xy):

plt.plot(xy[nnum][PX], xy[nnum][PY], "o")

nnum = nnum + 1

plt.title(fig_title + ' step = ' + str(i) + '/' + str(total_step))

def init_set(xy):

pnum = 0

xv_sum = 0

yv_sum = 0

particle_num = len(xy)

while pnum < particle_num:

xy[pnum][PX] = 0 # x-position

xy[pnum][PY] = 0 # y-position

xy[pnum][VX] = random.uniform(-1,1) # x-velocity

xy[pnum][VY] = random.uniform(-1,1) # y-velocity

xv_sum += xy[pnum][VX]

yv_sum += xy[pnum][VY]

xy[pnum][FX] = 0 # x-force

xy[pnum][FY] = 0 # y-force

pnum += 1

#Total momentum to zero

xv_sum = xv_sum / particle_num

yv_sum = yv_sum / particle_num

pnum = 0

while pnum < particle_num:

xy[pnum][VX] = xy[pnum][VX] - xv_sum

xy[pnum][VY] = xy[pnum][VY] - yv_sum

pnum += 1

if __name__ == "__main__":

fig = plt.figure(figsize = (10, 6))

fig.set_size_inches(10,10)

ax = fig.add_subplot(111)

perticle_num = 100

xy = [[0 for i in range(6)] for j in range(perticle_num)]

init_set(xy)

total_step =400

ani = anm.FuncAnimation(fig, \

update, fargs = ('Molecular Dynamics ', xy, total_step), \

interval = 10, frames = total_step)

plt.show()

#ani.save("Sample_MD.gif", writer = 'imagemagick', dpi=50)

実行の結果は下記。
Molecular dynamics simulation sample

2月 10, 2017

オンラインでのgif圧縮

matplotlibで生成したgifをwebへアップする際に、
少しでもgifファイルサイズを小さくするため下記サイトを使ってみた。

https://compressor.io/

結果は下記。余白が多いようなgifアニメは結構圧縮が効く様子。
930KB -> 530KB

2月 1, 20172月 5, 2017

cygwinでmatplotlibとscipyを使えるようにする

↓こちらのサイトを参考に、そのままの手順でできました。
http://ssmn0621.blogspot.jp/2016/03/cygwinnumpyscipymatplotlib.html

■pipのインストール
%easy_install-2.7 pip

■scipyのインストール
%pip install scipy

■matplotlibのインストール
%easy_install-2.7 matplotlib==2.0.0

■実行テスト
setenv DISPLAY :0.0 #DISPLAY設定
run xwin -multiwindow -noclipboard #xを起動
python rect.py

■実行結果
matplotlibで描画した長方形図形

■rect.pyの中身は↓

# -*- coding: utf-8 -*-
import matplotlib
import matplotlib.pyplot as plt

def main():
    fig = plt.figure()
    ax = fig.add_subplot(111)
    # 始点(0.2,0.2)で幅が0.2, 高さが0.4の長方形を描画
    rect = plt.Rectangle((0.2,0.2),0.2,0.4,fc="#770000")
    ax.add_patch(rect)
    plt.show()

if __name__ == '__main__':
    main()

# -*- coding: utf-8 -*-

import matplotlib

import matplotlib.pyplot as plt

def main():

fig = plt.figure()

ax = fig.add_subplot(111)

# 始点(0.2,0.2)で幅が0.2, 高さが0.4の長方形を描画

rect = plt.Rectangle((0.2,0.2),0.2,0.4,fc="#770000")

ax.add_patch(rect)

plt.show()

if __name__ == '__main__':

main()

※easy_install , pip
共にpython用外部ライブラリのパッケージ管理ツール
easy_installの方が古いらしく、pipはこれらを置き換える
　目的で開発されている。

1月 30, 2017

任意の数のランダムなxy座標を生成する

リスト形式でappendしてやることで、指定数を追加できる。
xyzならappendで追加する要素を３つにすればOK

#-*- coding:utf-8 -*-

import random

def init_xy(list,n):
    i = 0
    while i < n:
       list.append([random.random(),random.random()])
       i += 1


if __name__ == "__main__":
    n = 10
    xylist = []
    init_xy(xylist,n)
    print xylist

#-*- coding:utf-8 -*-

import random

def init_xy(list,n):

i = 0

while i < n:

list.append([random.random(),random.random()])

i += 1

if __name__ == "__main__":

n = 10

xylist = []

init_xy(xylist,n)

print xylist

1月 30, 20172月 10, 2017

関数に指定した引数は参照渡し

Pythonは関数に指定した引数がすべて参照渡しとなるらしい。
ただし、指定した引数の型によっては変更不可となる。

変更不可（イミュータブル）
int, float, str, tuple

変更可（ミュータブル）
list, set, dict

↓参考
http://docs.python.jp/2/reference/datamodel.html

■変更不可例

#-*- coding:utf-8 -*-

def test(gg):
    gg = gg * 2

if __name__ == "__main__":
    x = 10
    print(x)  ## 結果 10
    test(x)
    print(x)  ## 結果 10

#-*- coding:utf-8 -*-

def test(gg):

gg = gg * 2

if __name__ == "__main__":

x = 10

print(x) ## 結果 10

test(x)

print(x) ## 結果 10

■変更可例

#-*- coding:utf-8 -*-

def test(list):
    list[0] = list[0] * 2

if __name__ == "__main__":
    list = []
    list.append(10)
    print list[0]   ## 結果 10 
    test(list)
    print list[0]   ## 結果 20

#-*- coding:utf-8 -*-

def test(list):

list[0] = list[0] * 2

if __name__ == "__main__":

list = []

list.append(10)

print list[0] ## 結果 10

test(list)

print list[0] ## 結果 20

id関数を使ってみると、関数内でイミュータブル変数を変更すると識別子が変わった。
(ミュータブルは識別子変わらず)

#-*- coding:utf-8 -*-

def test(list,x):
    print id(list),id(x)   # 7696579635896 25769969816
    list[0] = list[0] * 2
    x += 1
    print id(list),id(x)   # 7696579635896 25769969792
if __name__ == "__main__":
    x = 1
    list = []
    list.append(10)
    print list[0],x       # 10 1
    print id(list),id(x)  # 7696579635896 25769969816
    test(list,x)
    print list[0],x       # 20 1
    print id(list),id(x)  # 7696579635896 25769969816

#-*- coding:utf-8 -*-

def test(list,x):

print id(list),id(x) # 7696579635896 25769969816

list[0] = list[0] * 2

x += 1

print id(list),id(x) # 7696579635896 25769969792

if __name__ == "__main__":

x = 1

list = []

list.append(10)

print list[0],x # 10 1

print id(list),id(x) # 7696579635896 25769969816

test(list,x)

print list[0],x # 20 1

print id(list),id(x) # 7696579635896 25769969816